探索式資料分析如何做?
探索式資料分析 (Exploratory Data Analysis, EDA) 是一套包含資料視覺化及統計等知識和技術的數據分析方法;其主要目的是從各個面向探索數據,找出解決問題的線索並進一步確認問題及解決方法。探索式資料分析通常沒有可依循的步驟,而是以一連串的啟發式的提問-回答的循環逐漸的釐清問題的核心,從數據中挖掘對問題深度的見解。
提問的問題,大致上可以從三個方向著手:
- 數據代表性
- 數據中的變數的分佈及變異為何?
- 各變數之間的關聯為何?
一、數據代表性:
收集到的數據是否足以代表要解決的問題的樣貌?拿到的數據就直接做分析,而沒先檢視數據的代表性,有可能會在一個錯誤的基礎上解決問題。
數據代表性的偏差來源有二種,一種是抽樣偏差 (sampling bias),另一種是倖存者偏差 (survivorship bias)。
抽樣偏差是指在抽樣時,某一群體的成員相較於其他群體有更高或更低的機率被抽選到,有時抽樣偏差是刻意設計而來的,譬如在製程管制中可能刻意挑選某些較能反應問題發生的區塊或時間來做檢驗;在分析這些數據時要能了解這些抽樣偏差所帶來的影響。
倖存者偏差則是指收集到的數據是經過某種過程或方法篩選出來的,因而最後的數據會遺失某些群體的資訊。著名的例子是二戰時的 Abraham Wald 分析轟炸機的防護問題,簡單講,在二戰時美國想要加強轟炸機的防護以增加存活率,所以開始對轟炸機所遭遇到的攻擊做研究以求有效的增強轟炸機承受攻擊的能力,但所收集到關於轟炸機所受攻擊的數據都來自於能返回的飛機,而沒有關於未能返回的轟炸機的資訊;但就加強轟炸機防護的這件任務,未能安全返回的飛機反而具有更高的數據價值,而Word 注意到這個現象,成功的做出正確的建議。倖存者偏差有時很難查覺,也不像轟炸機防護那麼容易做逆向推論,譬如像新產品開發時,大家會比較關注在有助於產品成功的因素,而忽略了讓產品失敗的因子,而這些失敗的因子很有可能會在量產時造成產品失效;附帶一提,有效的改善這種現象的方法是在開發過程即要注重落實 FMEA,而不能只是把 FMEA 當成品管文件。
在這個階段,試著問答:
- 數據是從何而來?收集到的數據可以代表要解決的問題的樣貌嗎?
- 抽樣的方法為何?有可能有抽樣偏差嗎?如果有,要如何處理?
- 可能有倖存者偏差嗎?要如何處理?
- 從持續改善的觀點,樣本偏差可以系統性的改善嗎?
- 如果樣本偏差是系統性的存在,那些在數據分析上可以做哪些系統性的處理?
二、數據中的變數的分佈及變異為何?
我們先簡單的說明幾個關鍵詞彙的意義。
- 變數:我們用變數來表示一個數值不固定的特性,例如,測量生產線上螺絲釘的長度,長度是螺絲釘的一個特性,而每根螺絲釘的長度也不會都一致,也就是螺絲釘長度這個特性是變動的,因而稱之為變數。螺絲釘長度是一個變數,螺牙間距則是另一個變數。
- 自變數和因變數:當我們試圖以一個(或多個)變數來解釋另外一個變數變化的原因,我們把前一種變數稱之為自變數,後一種變數稱之為因變數。即因變數受自變數的影響而改變,例如小學生的身高大致跟年齡成正向關聯,此時身高為因變數而年齡為自變數。
- 變異:變數的變動特性稱為變異。一般我們會計算變異數來表示一個變數的變異程度。
在這個階段,試著問答:
- 數據中有多少個變數?哪些是計數型變數?哪些是計量型變數?哪些分類型變數?分類型變數是否為有序?
- 數據有多遺失值?跟變數種類有無關聯?
- 遺失值會如何影響分析?甚至誤導分析的方向?
- 可以如何處理遺失值?移除含遺失值的條例或者應用數據插補 (data imputation)?
- 每個變數的數值分佈型態為何?可適用常態分佈?二項式或 Poisson 分佈?或其它數學型式的分佈?
- 每個變數的常態值或典型值為何?
- 每個變數的變異為何?
- 離群值或異常值為何?要如何處理?
- 離群值或異常值會如何影響分析?
- 是否有歷史紀錄可比較變數的分佈差異?例如某一個變數維持著跟過去差不多的分佈,或者有明顯的變化?
- 從持續改善的觀點,可以系統性的改善遺失值况異常值的發生嗎?
三、各變數之間的關聯為何?
在這個階段,試著問答:
- 變數中,有哪些是自變數?哪些是因變數?
- 自變數中,彼此相關 (共同變異) 的程度為何?如果某些自變數間有高度關聯性,要如何處理?
- 自變數中變異程度的差異為何?這些變異程度的差別會如何影響分析?
- 是否有多個因變數?如果有,這些因變數彼此是獨立的還是相關的?會如何影響分析?
- 因變數跟自變數間的關聯性?數據間的關聯態樣為何?若仔細探究每個變數中的子群,是否關聯的態樣就不同?
- 要如何描述因變數跟自變數間的關聯態樣?需要做統計檢定嗎?可以用數學模型表示嗎?
透過這三個面向的問題提問及探索解答,我們可以逐步的深入了解問題,進而正確的理解數據所呈現出來的特有型態,以及可能的解釋模型。
為達到這個目地,我們必須熟練的技能和工具有:
- 問題範疇的領域知識
- 統計知識:比較差異、回歸
- 數據分析軟體工具
EDA 基本技能介紹,以 R 語言為例
探索式資料分析需要高強度的分析工具使用技能。不論是套裝工具或程式軟體,分析人員要能熟練的以至少一種工具軟體才能有效率的進行數據探索及分析。以下我們用 R 語言介紹 EDA 常用的基本技能,包含:
- 概覧數據的結構
- 數據處理
- 數據視覺化
- 基礎統計
- 數據分析文件化
概覧數據的結構
先用 skimr 這個套件概略了解數據的結構,例如共有多少個變數?變數的種類?有無遺失值?基本統計資訊等等。
library(skimr)
skim(df)| Name | df |
| Number of rows | 3546 |
| Number of columns | 8 |
| _______________________ | |
| Column type frequency: | |
| character | 2 |
| numeric | 6 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| X2 | 0 | 1 | 2 | 2 | 0 | 3 | 0 |
| X3 | 0 | 1 | 2 | 2 | 0 | 2 | 0 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| X1 | 0 | 1.00 | 301.03 | 173.05 | 1.00 | 151.00 | 301.50 | 451.00 | 600.00 | ▇▇▇▇▇ |
| V1 | 159 | 0.96 | 102.04 | 10.54 | 66.80 | 94.96 | 101.75 | 109.12 | 136.01 | ▁▃▇▅▁ |
| V2 | 0 | 1.00 | 31.48 | 13.88 | 10.93 | 24.96 | 30.39 | 37.16 | 306.88 | ▇▁▁▁▁ |
| V3 | 0 | 1.00 | 116.86 | 15.33 | 78.05 | 103.87 | 116.06 | 129.73 | 154.84 | ▁▇▆▇▂ |
| V4 | 0 | 1.00 | 251.63 | 19.06 | 188.04 | 238.56 | 251.65 | 264.52 | 319.91 | ▁▅▇▃▁ |
| V5 | 0 | 1.00 | 116.69 | 31.86 | 30.01 | 91.15 | 113.33 | 141.30 | 212.59 | ▁▇▇▅▁ |
概覧這個 dataframe,共有 3546 行,8 個欄位;其中類別變數有兩個,數值型變數有6個。檢查變數的種類是否與預期中一致,若否,就要注意資料讀取參數的設定,或者在讀取數據之後強制轉換變數型態。
變數 X2 跟 X3 為類別型,X2 有3個 unique value (n_unique),X3有2個 unique value。
V1 含有 159 個遺失值,而 V2 數據分佈明顯偏右,這些現象值得再進一步仔細檢視。
數據處理
在整理數據時,一般會有兩大類的動作要做。第一類是搜尋、過濾、計算 dataframe 中的數據,第二類是轉換 dataframe 的形式。
先看第一類的數據整理動作,包含:
- 選擇欄位
- 過濾特定條件的資料列
- 用原有的數據產生新的欄位
- split-apply-combine: 將數據做分組 (split)、計算 (apply functions),然後再合併計算結果。
- 排序
找出遺失值 (NA values),並查看跟類別變數的關係。
library(tidyverse)
df %>% filter(is.na(V1)) %>% with(., table(X2, X3)) X3
X2 B1 B2
L1 27 40
L2 17 24
L3 28 23選擇特定欄位,顯示前 10 列。
df %>% select(X1, X2, X3, V3) %>% head(10) X1 X2 X3 V3
1 1 L1 B1 138.19122
2 1 L1 B2 107.19860
3 2 L1 B1 126.55454
4 2 L1 B2 102.22043
5 3 L1 B1 115.97476
6 3 L1 B2 97.96797
7 4 L1 B1 138.02288
8 4 L1 B2 105.94470
9 5 L1 B1 116.25192
10 5 L1 B2 112.45598用原有的數據產生新的欄位
df %>% select(X2, X3, V2, V3) %>%
mutate(Vn = V2 + V3) %>% head() X2 X3 V2 V3 Vn
1 L1 B1 26.58812 138.19122 164.7793
2 L1 B2 29.13510 107.19860 136.3337
3 L1 B1 27.38529 126.55454 153.9398
4 L1 B2 32.36461 102.22043 134.5850
5 L1 B1 29.47641 115.97476 145.4512
6 L1 B2 31.51080 97.96797 129.4788split-apply-combine: 把數據依 X2 的類別分組後,計算 V2 的平均值跟標準差,再將其合併成一 dataframe
df %>% select(X2, V2) %>%
group_by(X2) %>%
summarise(
mean = mean(V2),
st_dev = sd(V2)
)# A tibble: 3 x 3
X2 mean st_dev
<chr> <dbl> <dbl>
1 L1 30.1 3.59
2 L2 25.0 21.6
3 L3 39.0 3.38按照 V1, V2 的值,由小至大排序
df[1:10, ] %>% arrange(V1, V2) X1 X2 X3 V1 V2 V3 V4 V5
1 2 L1 B1 94.77810 27.38529 126.55454 250.7728 149.39813
2 1 L1 B1 98.51141 26.58812 138.19122 226.6297 151.19285
3 5 L1 B2 99.61112 27.77824 112.45598 256.7274 110.88601
4 4 L1 B2 100.79374 23.93658 105.94470 254.0335 97.10089
5 2 L1 B2 104.29365 32.36461 102.22043 262.9120 80.80640
6 3 L1 B1 105.32523 29.47641 115.97476 266.6994 113.65241
7 1 L1 B2 107.91134 29.13510 107.19860 255.1427 104.91676
8 4 L1 B1 108.62105 28.32014 138.02288 219.1680 172.98328
9 5 L1 B1 111.81220 33.04589 116.25192 241.3611 109.90543
10 3 L1 B2 114.56144 31.51080 97.96797 249.7458 74.05880第二類數據整理的動包含:
- 將一欄的值樞紐轉換 (pivot) 為數個欄位
- 將數個欄位的樞紐轉換為一個欄位
- 將一字元欄位的值直接分解為多個欄
- 將數個字元欄位的值直接合併為一欄
依照 X2 類別,把 V3 這一欄的值展開成多個欄位。
df_wide <- df %>% select(X1, X2, X3, V3) %>%
pivot_wider(names_from= X2, values_from= V3) %>% head()
df_wide# A tibble: 6 x 5
X1 X3 L1 L2 L3
<int> <chr> <dbl> <dbl> <dbl>
1 1 B1 138. NA 129.
2 1 B2 107. 98.7 113.
3 2 B1 127. NA 130.
4 2 B2 102. 96.9 110.
5 3 B1 116. 117. 136.
6 3 B2 98.0 103. 104.依照 X2 類別,把 V3 這一欄的值展開成多個欄位;之後把 L1 當成基準,計算L2、L3跟L1之間的落差。
df %>% select(X1, X2, X3, V3) %>%
pivot_wider(names_from= X2, values_from= V3) %>%
mutate(delta_L2 = L2 - L1,
delta_L3 = L3 - L1) %>%
head(10)# A tibble: 10 x 7
X1 X3 L1 L2 L3 delta_L2 delta_L3
<int> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 B1 138. NA 129. NA -9.61
2 1 B2 107. 98.7 113. -8.53 6.17
3 2 B1 127. NA 130. NA 3.86
4 2 B2 102. 96.9 110. -5.32 7.55
5 3 B1 116. 117. 136. 1.43 20.4
6 3 B2 98.0 103. 104. 4.84 6.05
7 4 B1 138. 150. 123. 11.5 -14.8
8 4 B2 106. 101. 102. -5.03 -4.03
9 5 B1 116. 140. 143. 23.5 26.5
10 5 B2 112. 113. 112. 1.02 -0.555將數個欄位的樞紐轉換為一個欄位。
df_wide %>%
pivot_longer(c("L1", "L2", "L3"), names_to = "item", values_to = "value") %>%
head()# A tibble: 6 x 4
X1 X3 item value
<int> <chr> <chr> <dbl>
1 1 B1 L1 138.
2 1 B1 L2 NA
3 1 B1 L3 129.
4 1 B2 L1 107.
5 1 B2 L2 98.7
6 1 B2 L3 113. 將數個欄位的字元直接合併為一欄,以 “-” 為連結符號
df_unite <- df %>% select(X2, X3, V1) %>%
unite(X2, X3, col= "item", sep= "-")
df_unite %>% head() item V1
1 L1-B1 98.51141
2 L1-B2 107.91134
3 L1-B1 94.77810
4 L1-B2 104.29365
5 L1-B1 105.32523
6 L1-B2 114.56144將一字元欄位的值直接分解為多個欄
df_unite %>%
separate(item, into = c("X2", "X3"), sep= "-") %>% head() X2 X3 V1
1 L1 B1 98.51141
2 L1 B2 107.91134
3 L1 B1 94.77810
4 L1 B2 104.29365
5 L1 B1 105.32523
6 L1 B2 114.56144數據視覺化
數據視覺化要能流暢的利用圖、表及文字標註呈現資訊的含義。我們是先提出問題,然後試著做出圖表看看是否能回答這個問題或產生另外的問題,再繼續以圖表探索,直到找出數據的涵義。這會需要知道各種圖表的用途,如何產生及解讀?如何利用形狀、顏色、線條、尺寸、空間軸向的安排?基本上,我們常透過圖形了解數據的分佈、組成、差異及關聯:
box-and-whisker plot: 看分佈的百分位數、快速找出異常或離群值
ggplot(df, aes(x= V2)) + geom_boxplot(outlier.shape= 4)
同時,也適快速比較不同群組間的分佈差異
ggplot(df, aes(x= X3, y= V3)) + geom_boxplot(outlier.shape= 4)
Violin plot: 是 box plot 的變形,它比 box plot 呈現出更多分佈形狀的訊息, 但少了離群值的資訊
ggplot(df, aes(x= X3, y= V3)) + geom_violin()
histogram: 檢視分佈的形狀,但需注意 bin 的大小通常會影響 histogram 的形狀
ggplot(df, aes(x= V3)) + geom_histogram(color= "white")
density plot: 檢視分佈形狀,是比 histogram 更好的選擇
ggplot(df, aes(x= V3)) + geom_density()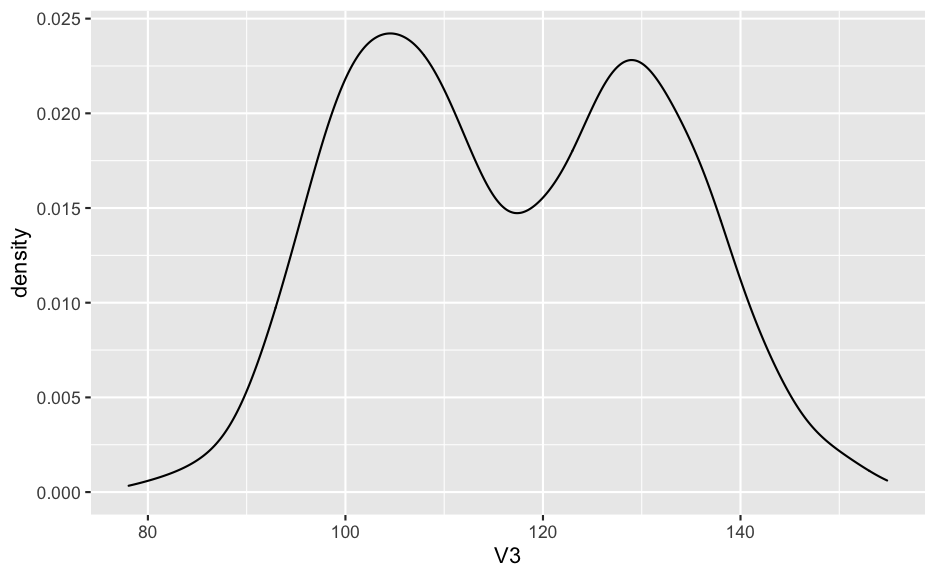
2D density plot: 二維的 density plot
df %>% filter(V2 < 100) %>%
ggplot(aes(x = V2, y = V3)) +
stat_density_2d(aes(fill = ..level..), geom = "polygon", colour="white")
bar chart: 檢視及比較組成
defects <- data.frame(
defect_type = c("A", "B", "C", "D"),
count = c(5, 12, 2, 6)
)
ggplot(defects, aes(x = defect_type, y = count)) +
geom_bar(stat = "identity")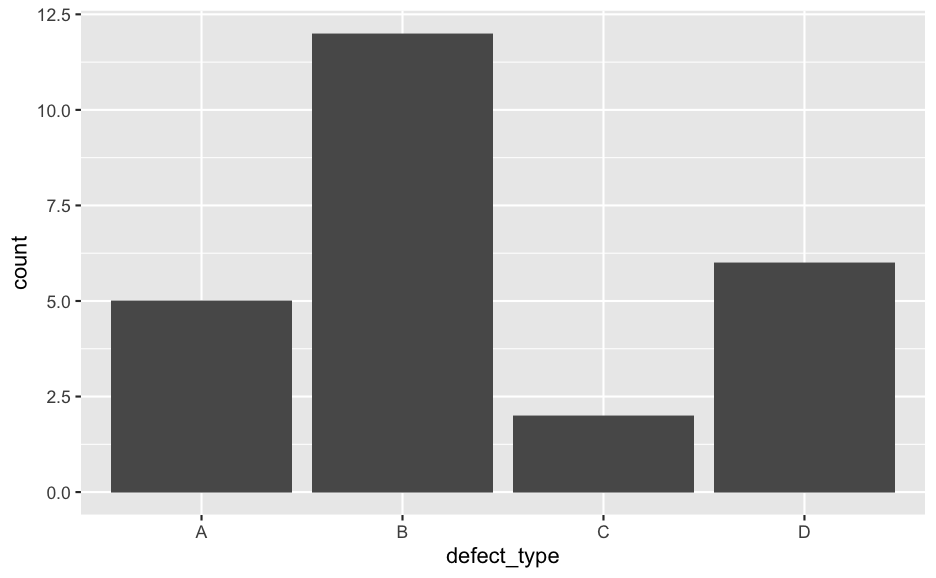
scatter chart: 檢視兩個變數間的關聯
df %>% filter(V2 < 100) %>%
ggplot(aes(x = V3, y = V5)) + geom_point()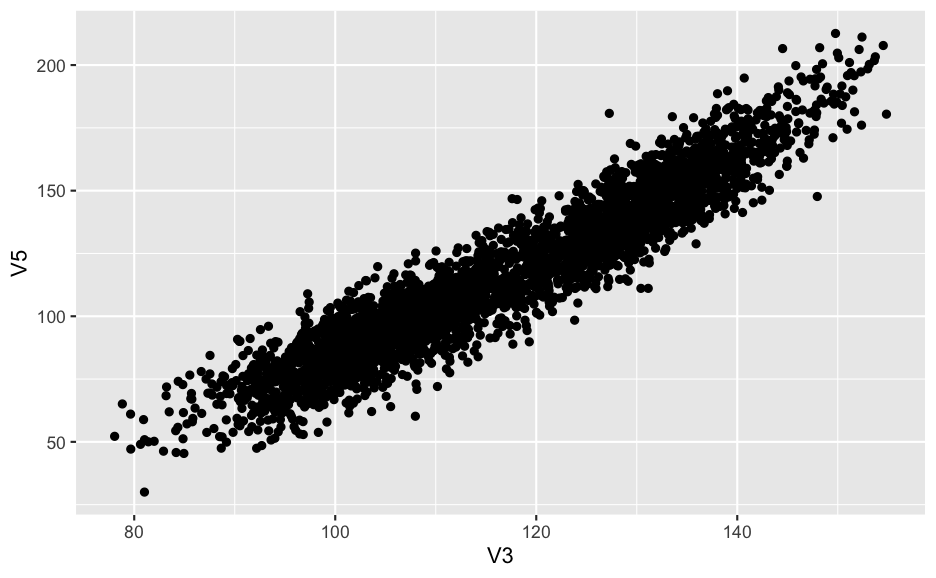
line chart: 顯示數據點間的連接性及變化
defects <- expand_grid(Week = paste0("W", 1:4),
defect_type = c("A", "B", "C", "D"))
defects$count <- sample(2:21, 16)
ggplot(defects, aes(x = Week, y = count, color = defect_type,
group = defect_type)) +
geom_point() + geom_line()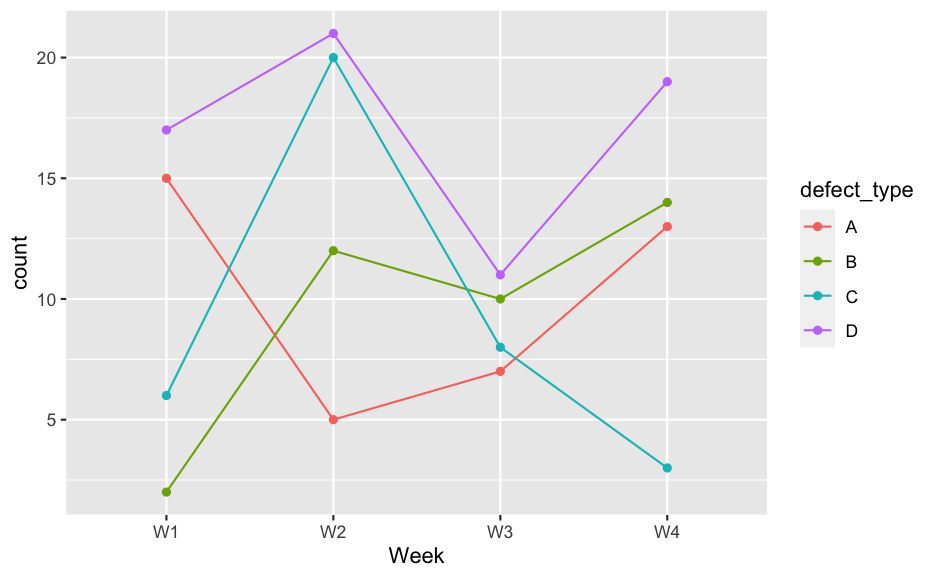
Line chart 最常被使用來呈現時間序列,線條連接表示兩個數據點之間的連結性。Line chart 跟 scatter chart 有不同的解讀意義,不可混用。
3D scatter chart: 檢視三個變數間的關聯
library(plotly)
df %>% filter(V2 < 100) %>%
plot_ly(x = ~V2, y = ~V3, z = ~V4)bubble plot: 以圓點尺寸表示第三維度的值
df %>% filter(V2 < 100) %>%
sample_n(100) %>%
ggplot(aes(x = V2, y = V4, size = V3)) +
geom_point(alpha = 0.5) +
scale_size(range = c(0.1, 10))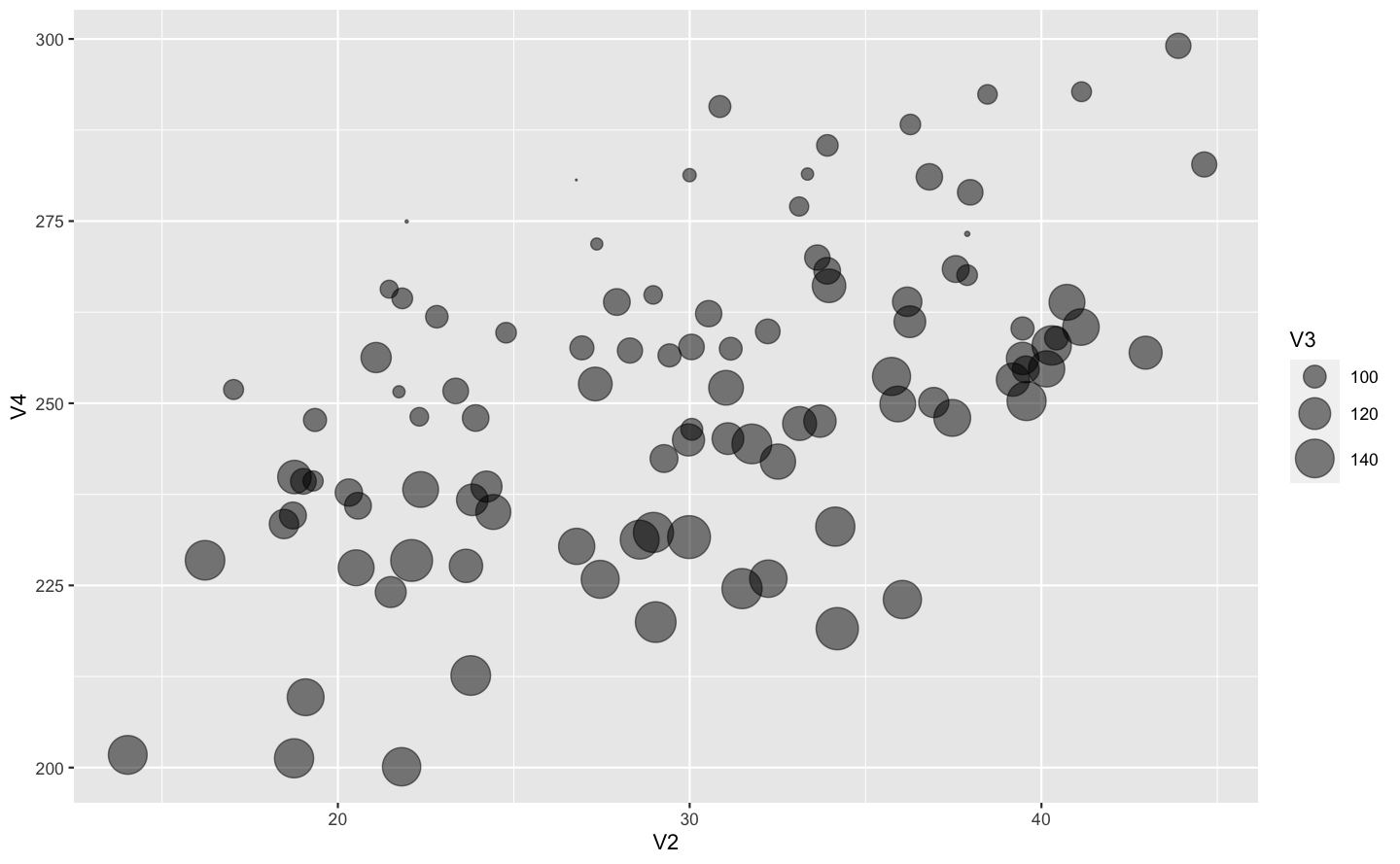
heat map: 以色調表示第三維度的值
defects <- expand_grid(product = paste0("P", 1:8),
defect_type = c("A", "B", "C", "D"))
defects$count <- sample(2:21, 32, replace = TRUE)
ggplot(defects, aes(x = product, y = defect_type, fill = count)) +
geom_tile() +
geom_text(aes(label = count))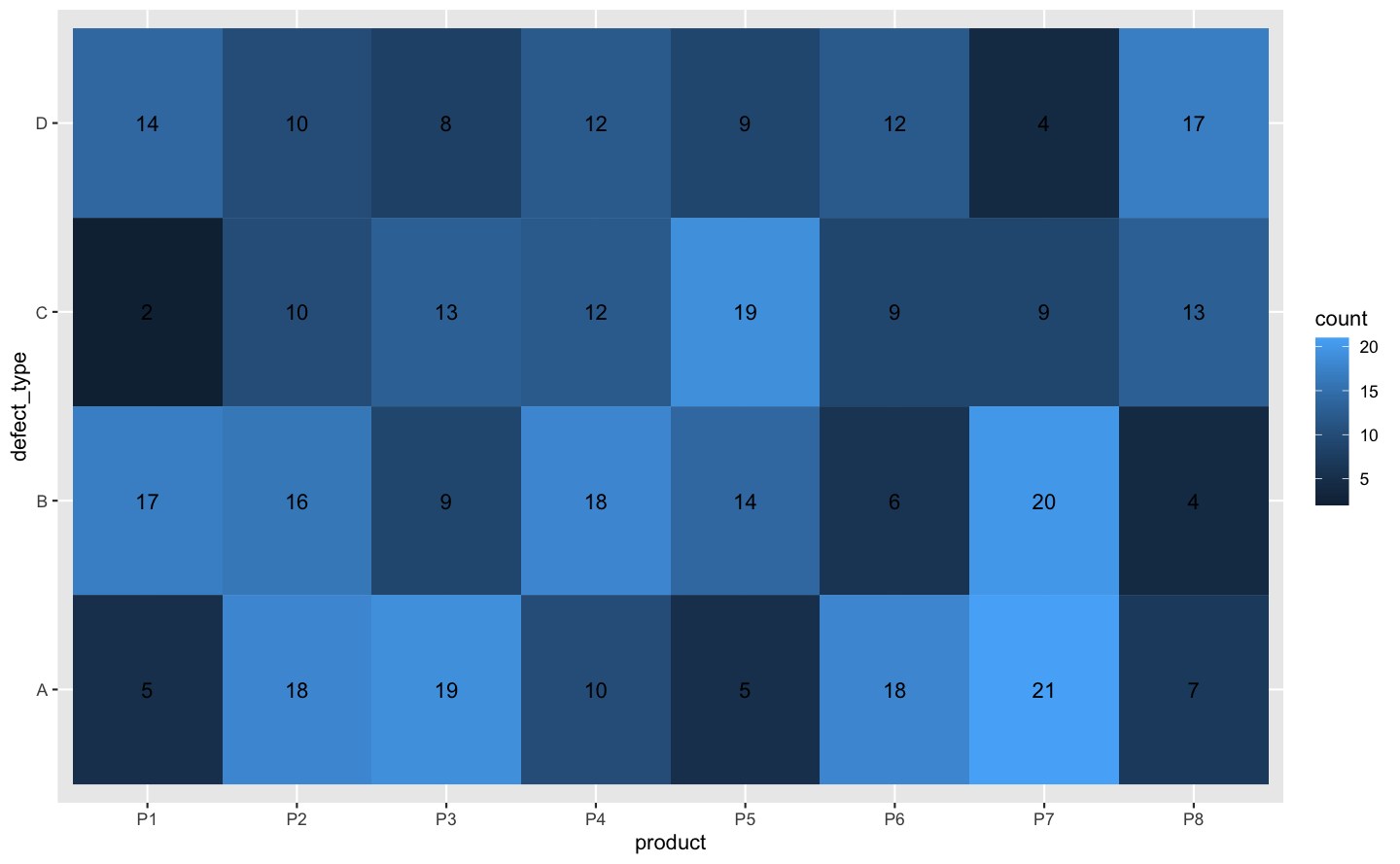
correlation matrix: 各變數之間的關聯矩陣圖
library(GGally)
df %>% filter(V2 < 100) %>%
select( V1, V2, V3, V4, V5) %>%
ggpairs()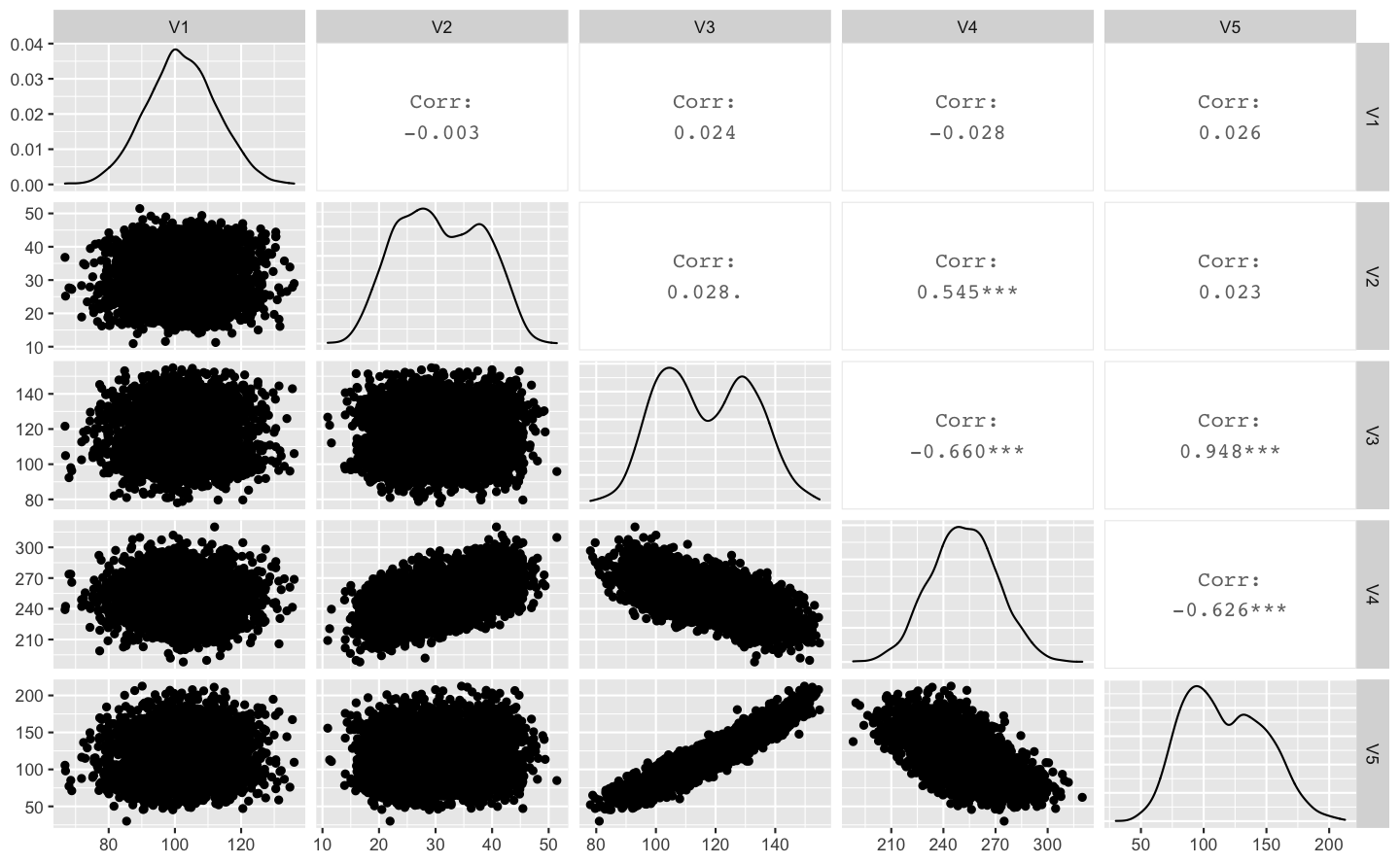
基礎統計
為了客觀的判斷由視覺化分析所得到的想法。我們可以藉由統計檢定、ANOVA及線性回歸來驗證差異跟關聯的顯著性;當然也要學會如何正確的使用統計方法及解讀分析的結果。
比較兩個平均值的差異
sample1 = rnorm(30, 101.2, 10)
sample2 = rnorm(30, 98.5, 10)
t.test(sample1, sample2)
Welch Two Sample t-test
data: sample1 and sample2
t = -0.78659, df = 57.1, p-value = 0.4348
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-6.681080 2.912472
sample estimates:
mean of x mean of y
99.47695 101.36125 當我們可以假設兩樣本群體都近似常態分佈,且變異程度相差不大;那麼相同的平均值意味著這兩個樣本群體是同一種型態。但注意,由於隨機變異的關係,我們認為的平均值相同並不是指兩個一樣的數值,而是以統計檢定來判斷。
比較多個平均值的差異
library(tidyverse)
data <- data.frame(sample1 = rnorm(30, 101.2, 10),
sample2 = rnorm(30, 98.5, 10),
sample3 = rnorm(30, 87.2, 10)) %>%
pivot_longer(c(sample1, sample2, sample3), names_to = "sample")
aov <- aov(value ~ sample, data)
summary(aov) Df Sum Sq Mean Sq F value Pr(>F)
sample 2 4374 2187.1 21.13 3.31e-08 ***
Residuals 87 9004 103.5
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1比較比例上的差異
假設有三個產品,各檢查 1000 件,各自發現有 52, 64, 72 個瑕疵品;這三種產品發生瑕疵的比例一樣嗎?
prop.test(x = c(52, 64, 72), n = c(1000, 1000, 1000))
3-sample test for equality of proportions without continuity
correction
data: c(52, 64, 72) out of c(1000, 1000, 1000)
X-squared = 3.4503, df = 2, p-value = 0.1782
alternative hypothesis: two.sided
sample estimates:
prop 1 prop 2 prop 3
0.052 0.064 0.072 測試相關性
defects <- data.frame(
row.names = c("product_1", "product_2"),
defect_A = c(34, 35),
defect_B = c(23, 12),
defect_C = c(43, 52),
defect_D = c(12, 6)
)
defects defect_A defect_B defect_C defect_D
product_1 34 23 43 12
product_2 35 12 52 6上方的表格代表著兩個不同的產品,各自檢查一千件所收集到的缺陷種類及數量的數據。我們想知道缺陷種類的分佈是否因產品而異?
chisq.test(defects)
Pearson's Chi-squared test
data: defects
X-squared = 6.1048, df = 3, p-value = 0.1066線性回歸:變數之間的線性關聯
df1 <- filter(df, ! is.na(V1), V2 < 100)
lm1 <- lm(V4 ~ V1 + V2 + V3, data = df1)
summary(lm1)
Call:
lm(formula = V4 ~ V1 + V2 + V3, data = df1)
Residuals:
Min 1Q Median 3Q Max
-35.465 -6.505 -0.382 6.662 34.151
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 307.28795 2.09415 146.74 <2e-16 ***
V1 -0.01872 0.01546 -1.21 0.226
V2 1.44852 0.02196 65.95 <2e-16 ***
V3 -0.84254 0.01060 -79.48 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 9.459 on 3373 degrees of freedom
Multiple R-squared: 0.7558, Adjusted R-squared: 0.7556
F-statistic: 3481 on 3 and 3373 DF, p-value: < 2.2e-16數據分析文件化
結合 R scripting 的分析程式化跟 markdown 的文件功能,我們可以文件化數據分析的過程及結果。
由於 R script 紀錄了從數據讀取、整理、分析、視覺化過程的所有程式碼,不再是零碎的分析然後再人工組成報告,所以保持了分析過程及方法的一致性,同時也由於程式自動化執行分析及輸出 HTML 或 PDF 的報告至指定路徑,所以用 R 或 python 程式語言進行數據分析會具有了下列的優點:
- 再現性的 (reproducible)分析報告。
- 數據分析的合作討論平台。
- 對於複雜的數據分析專案,大力促進分析的效率。
- 有助於企業的知識管理。
對於想要建立數據智能的企業而言,與其一開始就花大錢建立AI、大數據的設施,找一群AI/機器學習工程師或數據科學家;比較務實的做法或許是先推行規模比較小的改善計劃,在過程中逐步建立企業數據分析的能力,摸索及釐清企業對數據智能的目標及需求,再依據需求建置數據設施跟數據人才。有了穩固數據分析基礎及較成熟的企業數據素養,在AI或智慧製造上的投資才會有更好的回收。此外,當有了大規模的數據設施後,企業也容易聚焦在大型的數據專案上,由 EDA 產生的知識還是很容易的散落在各個工程師手中,防礙企業知識整合應用。
探索式資料分析是所有分析的基礎。從工廠日常的工程分析到高階的AI預測模型,都少不了探索式資料分析的基本工。